Unit 1: An Introduction to the Unified Coherence Field

• Qiskit Courses
• Bra-Ket Notation
  • How to Write them in Latex / MathJax
• 1.0 Introduction: Beyond Classical Intuition
• 2.0 The "Source Code": Qubits as the Foundation of Quantum Information
  • Analysis of the Qubit
• 3.0 The "Engine": Process Theories and Composition
  • Deconstruction of the Process Engine
• 4.0 The "Lock": Symmetry, Palindromes, and Structural Stability
  • Analysis of Quantum Symmetry
• 5.0 The "Map": The Role of Complex Numbers and Phase
  • Exploration of the Complex Plane
• 6.0 The "Goal": Achieving Coherence and Non-Separability
  • Synthesis of Coherence
• 7.0 Glossary of Terms

Qiskit Courses

Understanding Quantum Information & Computation With John Watrous

The goal for this series is simple: to create a university level quantum course and to make it available worldwide, while explaining how quantum information ...

Introduction to Quantum Computing and Quantum Hardware

This course is an introduction to the world of quantum computing, with an exploration of some of the key quantum algorithms and their implementations using q...

Bra-Ket Notation

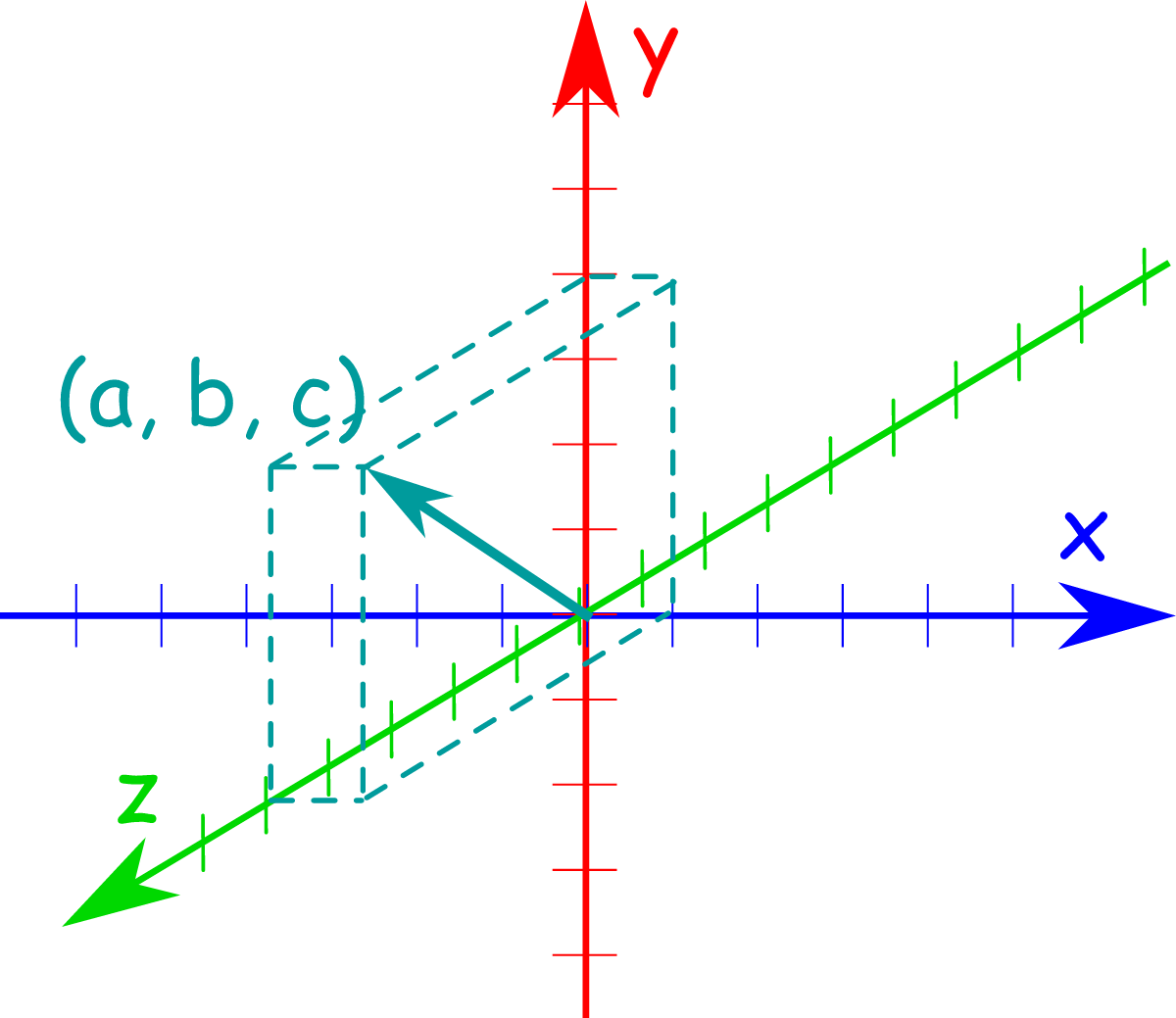
Vector in Three Dimensions

Bra-Ket Notation

Also called Dirac Notation. Bra-Ket is a way of writing special vectors used in Quantum Physics that looks like this:

$|Kets⟩$

We can write this as a column vector like this:

$r=\left[\begin{array}{c}a\\ b\\ c\end{array}\right]$

Or we can write it as a "ket":

$|r⟩=\left[\begin{array}{c}a\\ b\\ c\end{array}\right]$

But kets are special

• The values (a, b and c above) are complex numbers (they may be real numbers, imaginary numbers or a combination of both)
• A ket is a quantum state
• Kets can have any number of dimensions, including infinite dimensions!

The "bra" is similar, ==but the values are in a row, and each element is the complex conjugate of the ket's elements.==

Example

This Ket:

$$|a⟩=\left[\begin{array}{c}2-3i\\ 6+4i\\ 3-i\end{array}\right]$$

Has this bra

$$⟨a|=\left[\begin{array}{ccc}2+3i& 6-4i& 3+i\end{array}\right]$$

The values are now in a row, and we also changed the sign (+ to −, and − to +) in the middle of each element.

In "matrix language", changing a ket into a bra (or bra into a ket) is a "conjugate transpose":

• conjugate: 2−3i becomes 2+3i, and so on...
• transpose: rows swap with columns

Read more at Matrix Types.

Multiplication of $⟨a|$ and $|b⟩$

$⟨a|b⟩$

We use matrix multiplication, in particular the dot product:

Example

The "Dot Product" is where we multiply matching members, then sum up:

$$\left[\begin{array}{ccc}1& 2& 3\end{array}\right]\left[\begin{array}{c}7\\ 9\\ 11\end{array}\right]=(1\times 7)+(2\times 9)+(3\times 11)=58$$

We match the 1st members (1 and 7), multiply them, likewise for the 2nd members (2 and 9) and the 3rd members (3 and 11), and finally sum them up.

How to Write them in Latex / MathJax

$⟨\varphi |$

$\bra{\phi}$

1.0 Introduction: Beyond Classical Intuition

Welcome. The purpose of this course is to explore the fundamental nature of reality. To do so, we must first recognize that our conventional, classical ways of thinking—the intuitions we have built from observing the macroscopic world—are profoundly insufficient for this task. The rules that govern the universe at its most basic level operate on a logic that is entirely different from our everyday experience.

We will come to understand that quantum theory is not merely a collection of strange and counter-intuitive rules, but rather a new "operating system" for reality itself. This system is built on a trinity of foundational principles: information, the basic currency of existence; interaction, the engine through which information evolves; and composition, the set of rules for how systems combine to form more complex wholes. This unit is designed to deconstruct this operating system into its five core components. To make its logic intuitive and its structure clear, we will employ the source's novel visual language, which reveals how this 'code' builds 'engines' and 'locks' not with algebra, but with pictures.

2.0 The "Source Code": Qubits as the Foundation of Quantum Information

To understand any operating system, we must begin with its most fundamental unit of information—its source code. In classical computing, this unit is the bit. In the quantum world, it is the infinitely richer and more complex qubit. The distinction between these two is not merely a matter of degree; it represents a fundamental divergence in how reality stores and processes information, and it is the primary reason the quantum world is capable of phenomena that seem impossible from a classical perspective.

Analysis of the Qubit

A classical bit, the foundation of all digital technology, is a model of simplicity. It operates under a few straightforward rules:

1. It admits only two discrete states, which we label 0 and 1.
2. It can be subjected to any function, such as the NOT function, which swaps 0 and 1, or a constant 0 function, which maps both states to 0.
3. It can be freely read without obstruction and without altering its state.

The quantum bit, or qubit, operates under a radically different and more expansive set of principles.

1. A Sphere of States: A qubit does not have just two states; it admits an entire sphere of possible states. To visualize this, we can use the analogy of the Earth, what physicists call the Bloch Sphere. If we place the classical state 0 at the North Pole and 1 at the South Pole, the qubit can exist not only at these two points but at any point on the surface of the globe. It has an infinite, continuous state space.
2. Restricted Operations: Unlike a classical bit, a qubit cannot be subjected to any arbitrary function. The only permissible operations are rotations of this sphere. This has a profound consequence: it is impossible to map all states to a single state. There is no rotation that can take every point on the Earth's surface and move it to the North Pole. This inherent restriction preserves the richness of the quantum state space.
3. The Invasion of Measurement: Perhaps the most jarring departure from classical intuition is the act of reading a qubit's state. In the quantum realm, there is no such thing as passive observation. The act of measurement is an invasive, disruptive, and fundamentally non-deterministic process.
4. To grasp this, consider the analogy of "Dave the Dodo," a quantum system whose state is a location on Earth—say, Oxford. If we want to measure Dave's state, we are restricted to asking a binary question, such as, "Are you at the North Pole or the South Pole?" Dave, being a dodo, will give an answer. But the moment he answers, his statement becomes true. If he says "North Pole," he is instantly at the North Pole. His original state in Oxford is permanently and irretrievably lost. This phenomenon is known as the collapse of the quantum state. The measurement has fundamentally altered the system. We can never know with certainty where Dave will end up; quantum theory only provides us with the probabilities of him collapsing to one pole or the other.

With this understanding of the fundamental unit of quantum information—the code—we can now turn to the rules that govern how these units interact and evolve. We must examine the system's engine.

3.0 The "Engine": Process Theories and Composition

The true power of quantum theory does not reside in its static states, but in its dynamic processes. As Erwin Schrödinger observed, it is the interaction and composition of systems that reveals the most profound features of the quantum world. He wrote, "I would not call that one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought." To understand this, we must shift our focus from what a system is to what it does—from states to the processes that transform them. This shift requires a new framework, one where interaction is the central object of study.

Deconstruction of the Process Engine

This new framework is built on the concept of a process theory.

• A process is any transformation with inputs and outputs. We can visualize it as a simple "box" with incoming "wires" (inputs) and outgoing "wires" (outputs). This simple abstraction moves our focus from static objects ('what is') to dynamic actions ('what happens').
• A process theory is the complete set of rules governing these transformations. It consists of a collection of allowed system-types (the wires), a collection of allowed processes (the boxes), and a well-defined means of wiring them together. In this framework, the absolute position of a box is irrelevant; what matters is its connectivity.

Processes can be combined, or composed, in two fundamental ways:

1. Parallel Composition (**⊗**): This describes processes that occur side-by-side, independently of one another. We place the boxes next to each other.
2. Sequential Composition (**∘**): This describes processes that occur one after another, where the output of the first process becomes the input of the second. We stack the boxes vertically.

This compositional structure is why a diagrammatic language is not just a helpful illustration but a superior formalism for this new physics. A diagram makes the flow of interaction intuitive and self-evident. Traditional algebraic formulas, by contrast, are "unwieldy" and "bureaucratic." They force us to compress a two-dimensional reality of parallel and sequential interactions onto a one-dimensional line of symbols, requiring extra rules to manage the complexity. For instance, the self-evident nature of the diagram below must be explicitly stated in algebra by an axiom known as the interchange law: (g1 ⊗ g2) ∘ (f1 ⊗ f2) = (g1 ∘ f1) ⊗ (g2 ∘ f2).

Algebraic Representation	Diagrammatic Representation
(g₁ ⊗ g₂) ∘ (f₁ ⊗ f₂)	A diagram showing two processes, f₁ and f₂, side-by-side. Their outputs connect directly to the inputs of two subsequent processes, g₁ and g₂, also side-by-side.

The diagram speaks for itself; the algebra requires a translator.

Now that we have the source code (qubits) and the engine that runs it (process theories), we need to understand the structural rules that provide stability and allow for repeatable, predictable operations. We need to find the system's locks.

4.0 The "Lock": Symmetry, Palindromes, and Structural Stability

For any information system to be coherent and useful, it must possess points of stability and symmetry—anchors in the dynamic flow of processes. The source material's reference to a book on gene editing hints at a deeper pattern: nature often relies on structural symmetry for its most fundamental processes. The simplest version of this is a palindrome, a sequence like 'RACECAR' that reads the same forwards and backwards. This concept of forward/backward symmetry finds a powerful and more abstract analogue in the diagrammatic language of quantum processes.

Analysis of Quantum Symmetry

In our diagrammatic language, the simple "forward/backward" symmetry of a palindrome is elevated into more abstract but equally powerful symmetries:

• Adjoints (**†**): The adjoint of a process corresponds to a vertical reflection of its diagram. Operationally, this is a profound transformation. It turns a state-preparation process (e.g., creating a qubit in state |ψ⟩) into its corresponding "testing" process (⟨ψ|). This new process doesn't create the state; it verifies if a given system is already in that state. It is the question to the original statement.

Process (|ψ⟩)	Adjoint (⟨ψ|) (Vertical Reflection)
A triangle pointing up, with a single wire emerging from its top vertex.	A triangle pointing down, with a single wire entering its bottom vertex.

• Transpose (**T**): The transpose of a process corresponds to a 180-degree rotation of its diagram. This flips the diagram upside-down, turning inputs into outputs and outputs into inputs.

While both represent a form of quantum 'palindromic' symmetry, the Adjoint (vertical reflection) speaks to the relationship between preparing and testing a state, while the Transpose (180° rotation) speaks to the relationship between a process and one where all inputs and outputs are swapped.

These symmetries provide the "locks" of the quantum operating system. A process that is its own adjoint or its own transpose is "palindromic" in a quantum sense. It represents a point of perfect structural stability or a fundamental symmetry in the system's dynamics. These self-symmetric processes, like palindromes in language, are not just curiosities; they are foundational anchors that make complex quantum operations possible.

Having established the structural rules, we must now turn to the mathematical language required to map the full, rich dynamics of quantum states, including subtle properties like spin and phase.

5.0 The "Map": The Role of Complex Numbers and Phase

The simple, one-dimensional real number line, which describes quantities in terms of "forward" and "backward," is insufficient to map the full behavior of quantum systems. The world of qubits is not a line between two poles but a sphere. To describe motion on this sphere—not just between north and south but along the equator—we must expand our mathematical language to include a second dimension: rotation, or what physicists call phase. This is the essential role of complex and imaginary numbers in quantum theory.

Exploration of the Complex Plane

Real numbers can be visualized as points on a line. Complex numbers extend this to a two-dimensional plane, incorporating a vertical "imaginary" axis. This extra dimension is precisely what quantum theory needs to describe its complete reality.

The reason quantum theory requires complex numbers is that quantum states are defined not just by their magnitude (how far from the origin) but also by their phase (their angle of rotation around the origin). Returning to our Bloch sphere analogy for the qubit:

• Movement along the line of longitude between the North Pole (0) and the South Pole (1) can be described with real numbers.
• However, to describe states along the equator—which represent perfect superpositions of 0 and 1—we need an additional parameter. All points on the equator are equidistant from the poles, but they are distinct states. What distinguishes them is their phase, which corresponds to their longitude. Complex numbers provide the natural language for describing this rotational degree of freedom.

The phase is not a superficial detail; it is a fundamental component of a quantum state that governs how it interferes with other states. Without complex numbers to serve as the map, the rich, subtle, and powerful dynamics of quantum interference would be impossible to describe.

With the code, engine, lock, and map now defined, we are finally ready to synthesize them into a complete picture and understand the system's ultimate goal.

6.0 The "Goal": Achieving Coherence and Non-Separability

The ultimate purpose of this quantum operating system is not merely computation in the classical sense. Its goal is to achieve a state of profound interconnectedness known as Coherence, a state in which the constituent parts of a system become linked in a way that transcends the boundaries of classical physics. In this state, the whole truly becomes more than the sum of its parts.

Synthesis of Coherence

The core concept that enables this state is Non-Separability. As Schrödinger identified, "I would not call that one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought." It means that a coherent, multi-part quantum system can no longer be described by considering each of its components individually. The information defining the system is not stored in the parts but in the intricate relationships between them.

Our diagrammatic language provides a beautiful and intuitive representation of this concept through "cups" (**∪**) and "caps" (**∩**). These are not processes in the traditional sense but are visual representations of non-separable, or entangled, states. They are the wires that bind systems together in a way that makes them inseparable. A "cup" is a U-shaped wire that turns two outputs into a correlated pair. A "cap" is an inverted-U that does the same for two inputs.

We can now define Coherence as the synthesis of the four components we have explored:

• Coherence is built upon the Code of qubits, whose capacity for superposition provides the raw material for non-classical states.
• This potential is realized through the Engine of interaction, where processes compose and wire systems together, creating correlations that did not previously exist.
• These correlations are given stability and structure by Locks—fundamental symmetries like adjoints—which are the diagrammatic anchors, such as cups and caps, that represent perfectly entangled states.
• This entire structure is navigated using the Map of complex numbers, where phase becomes the essential coordinate for defining the precise, intricate relationships that constitute a coherent system.

When a system achieves this state of Coherence, it becomes a gateway to the most powerful and non-classical features of the quantum world. As described in the source materials, it is this non-separable, coherent state that makes seemingly impossible phenomena like quantum teleportation and non-locality a reality. These are not magic tricks; they are the logical consequences of an operating system founded on coherence.

This unified, coherent state, born from the interplay of information, interaction, and symmetry, is the true source of the "unthinkable power" latent in the quantum realm.

7.0 Glossary of Terms

Term	Definition
Qubit	The fundamental unit of quantum information. Unlike a classical bit (0 or 1), a qubit can exist in a continuous sphere of states, including superpositions of 0 and 1.
Process Theory	A framework for describing physical systems based on transformations (processes) rather than static states. It consists of system-types (wires), allowed processes (boxes), and rules for their composition.
Composition (Sequential & Parallel)	The way processes are combined. Sequential composition (∘) is one process followed by another, while Parallel composition (⊗) is two processes occurring side-by-side.
String Diagram	A diagrammatic language for quantum processes that uses "cups" and "caps" to represent non-separable (entangled) states, allowing wires to bend and connect inputs to inputs or outputs to outputs.
Non-Separability (Entanglement)	A state of a multi-part quantum system where the parts are so deeply correlated that they cannot be described independently. It is "the characteristic trait of quantum mechanics."
Adjoint (**†**)	The vertical reflection of a process diagram. It operationally transforms a state-preparation process (`
Transpose (**T**)	The 180-degree rotation of a process diagram. It operationally turns a process's inputs into outputs and vice versa.
Inner Product	A number obtained by composing a state with the adjoint of another (`⟨φ
Unitarity	A property of a process that is reversible and preserves the inner product. A process is unitary if its adjoint is also its inverse (U† ∘ U = 1 and U ∘ U† = 1).
Quantum Measurement	An invasive, non-deterministic process that extracts limited information from a quantum system, causing its state to "collapse" into one of the possible outcomes.